---
engine: julia
---
# Diamond-Mortensen-Pissarides Framework
```{julia}
#| label: setup-dmp
#| output: false
#| code-fold: true
using ProjectRoot
using DataFrames
using StatsPlots
using QuantEcon: hp_filter
using MacroModelling: @model, @parameters, get_simulation, plot_irf, get_steady_state, get_irf, get_parameters
using Statistics
using PrettyTables
using Printf
using CSV
import Random
Random.seed!(1234)
mypalette = ["#d5968c", "#c2676d", "#5c363a", "#995041", "#45939c", "#0f6a81"]
default(size=(600, 370), titlefontsize=10, fmt=:svg, grid=false,
foreground_color_legend=nothing, palette=mypalette[[6, 2, 4, 3, 1, 5]])
```
## DMP Framework とは
これまで見てきたモデルでは, 摩擦のない労働市場を前提としていました. つまり, 全ての企業は労働者を雇うことができ, 労働者は均衡賃金で仕事を見つけられると仮定していました. しかし, 実際の労働市場では失業, 働きたいが仕事が見つからない, といった現象が観察されます. DMPモデルは, こうした摩擦のある労働市場を考慮し, 失業を内生化するモデルです.
DMPモデルは, 今まで学んできた Solow, Ramsey, RBC, New Keynesian モデルの流れと直接のつながりがないため, 少し違和感を感じるかもしれません. しかし, その後の研究で, DMPモデルはこれら新古典派のモデルと組み合わされていき [@merz1995; @andolfatto1996], 代表的な研究として @krusell2010 のモデルがあります.
ちなみに, Diamond, Mortensen, Pissarides の3人は, 2010年にノーベル経済学賞を受賞しています.
](/static/img/03-dmp/nobel2010.png){#fig-nobel2010 width=80% }
## Stylized Facts
**失業の定義**
失業は16歳以上の労働力人口を以下の3つに分類して定義されます.
- $E$: Employed. 仕事を持っている人
- $U$: Unemployed. 仕事を持っていないが, 仕事を探している人
- $N$: Not in the Labor Force. 仕事を持っておらず, 仕事も探していない人
例えば, 学生や専業主婦, 引退した高齢者などが $N$ に該当します. 失業率 $u_t$ は以下のように定義されます.
$$
u_t := \frac{U_t}{E_t + U_t}
$$
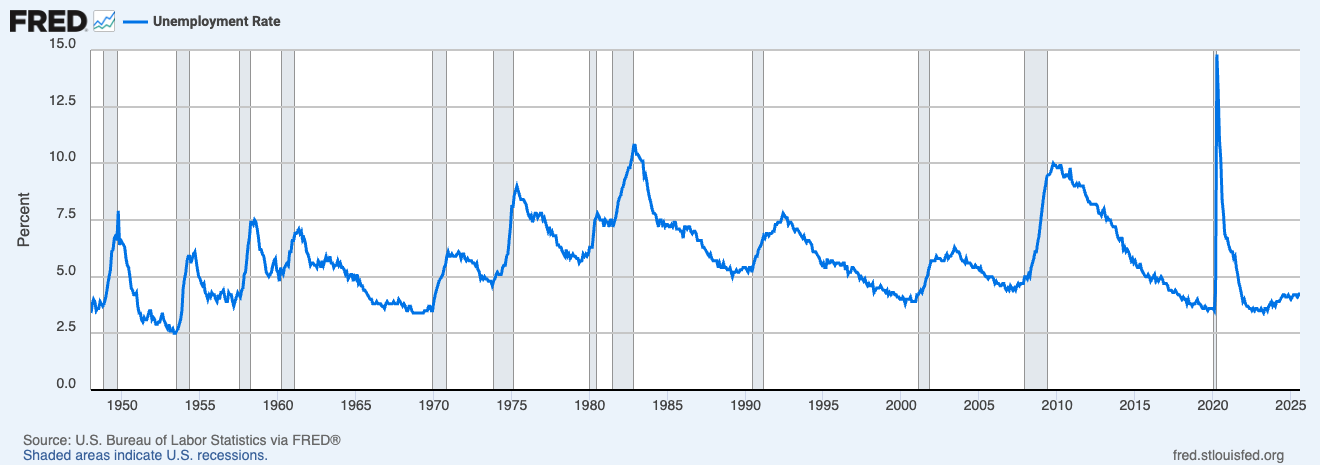
.](/static/img/03-dmp/fred_unrate.png){#fig-unrate width=100% }
@fig-unrate はアメリカの失業率とNBERによる不況期間 (グレー) を示しています. 失業率は不況期に上昇し, 景気回復期に低下する傾向があることがわかります.^[NBERの[Business Cycle Dating](https://www.nber.org/research/business-cycle-dating) には雇用に関する指数も含まれているため, ある意味当然の結果とも言えます.]
## Model
### 設定
- 労働者は Employed ($E$) か Unemployed ($U$) のいずれかの状態にある
- それぞれの状態にある労働者の数を $e_t$ と $u_t$ とし, $e_t + u_t = 1$
- $E$ から $U$ への遷移確率を $\sigma$ とし, $U$ から $E$ への遷移確率を $\lambda$ とする
{#fig-model-eu width=80% }
よって失業率 $u_t$ の遷移は次のように表されます.
$$
u_{t+1} = (1-\lambda)u_t + \sigma (1-u_t).
$$
Steady state $u_{t+1} = u_t = \overline{u}$ について解くと,
$$
\overline{u} = \frac{\sigma}{\lambda + \sigma}.
$${#eq-ss-unemployment}
### マッチング関数
::: {.callout-note}
## マッチング関数
$t$ 時点における失業者の数を $u_t$, 求人の数 (vacancy) を $v_t$ とした時, $t+1$ の始めにおけるマッチの数 $\mathcal{M}_{t+1}$ は次のように表されます.
$$
\mathcal{M}_{t+1} = M(u_t, v_t).
$$
このマッチング関数 $M(u, v)$ は以下の性質を持ちます.
- $u, v$ に対して単調増加
- Constant returns to scale
- $M(u, v) \le u, v$
:::
このマッチング関数は _Blackbox_ な関数と言われます. 雇用に際しどのような要因でどのような摩擦があるのかなどに深入りせず, それらの摩擦を吸収した抽象的な関数として考えます.
労働者 (worker) が企業にマッチする確率は $\lambda_w$ は以下のように表されます.
$$
\lambda_w(\theta_t) = \frac{M(u_t, v_t)}{u_t} = M\left(1, \frac{v_t}{u_t}\right) = M(1, \theta_t).
$$
この $\theta_t := \frac{v_t}{u_t}$ は労働市場の逼迫性 (labor market tightness) と呼ばれます. 例えば, 労働市場がタイト, $\theta_t$ が大きい場合, 求人が多く失業者が少ないことを意味し, 雇い主は高い賃金を提示して雇用しなければなりません. 逆に, 労働市場が緩和, $\theta_t$ が小さい場合, 求人が少なく失業者が多いことを意味し, 雇い主は低い賃金でも労働者を雇うことができます. これを @eq-ss-unemployment に代入すると,
$$
\overline{u} = \frac{\sigma}{\lambda_{w}(v / \overline{u}) + \sigma}
$$
であり, 変形すると
$$
M(\overline{u}, v) + \sigma \overline{u} = \sigma.
$${#eq-beveridge-curve}
この関係から, $\sigma$ が定数であれば, (定常状態の) 失業率 $\overline{u}$ と 求人 $v$ に負の関係があることがわかります. この関係を, **ベバリッジ曲線** (Beveridge Curve) と呼びます.
なお, 求人 $v_t$ がマッチする確率を $\lambda_f$ とすると,
$$
\frac{M(u_t, v_t)}{v_t} = M\left(\frac{u_t}{v_t}, 1\right) = M\left(\frac{1}{\theta_t}, 1\right) =: \lambda_f(\theta_t).
$$
### ベバリッジ曲線とシフト
![**Beveridge Curve in the United States** [@azzimonti2025, fig. 20.4]](/static/img/akmm/chapter19/fig4.svg){#fig-bc-us}
@fig-bc-us は2000年以降のアメリカのベバリッジ曲線を示しています. グラフの中で, 3つのベバリッジ曲線 Dec. 2000 - Oct. 2009, Oct. 2009 - Apr. 2020, Apr. 2020 - May 2022 とその間のシフトを見ることができます. シフトが起こった時期は, リーマンショックやCovid-19の影響を受けた時期です.
ベバリッジ曲線のシフトの一つの解釈はマッチング関数の変化です. 例えば, マッチング関数が以下のコブ・ダグラス型であるとすると
$$
M(u, v) = \chi u^\eta v^{1-\eta},
$${#eq-matching-cobb-douglas}
ベバリッジ曲線は以下のように表されます.
$$
v = \left(\frac{\sigma (1-\overline{u})}{\chi \overline{u}^{\eta}}\right)^{\frac{1}{1-\eta}}.
$$
マッチングのしやすさを表す $\chi$ が小さくなったとき, ベバリッジ曲線が上にシフトすることがわかります.
### 労働市場均衡
ここで, 求人 $v_t$ が決定する労働市場の均衡を考えます.
**企業**
- 無限期間の利益を最大化すると考える. 割引率を $\beta \in (0, 1)$ とする
- $t$ 期の生産を $z_t$ とし, マルコフ過程に従うとする
- 労働者に払う賃金を $w(z)$ とする
- 求人を出すコストを $\kappa$ とする
十分な労働者がいる企業の価値関数を $J(z)$, 求人を行う企業の価値関数を $V(z)$ とすると
$$
\begin{aligned}
J(z) &= z - w(z) + \beta \mathbb{E}\left[(1-\sigma)J(z') + \sigma V(z') \mid z\right] \\
V(z) &= -\kappa + \beta \mathbb{E}\left[(1-\lambda_f(\theta))V(z') + \lambda_f(\theta) J(z') \mid z\right].
\end{aligned}
$${#eq-bellman-firm}
ここでは, 企業が労働者にマッチする確率を $\lambda_f(\theta)$ とし,
$$
\lambda_f(\theta) = \frac{M(u, v)}{v} = M\left(\frac{u}{v}, 1\right) = M\left(\frac{1}{\theta}, 1\right).
$$
さらに, 求人はどの企業も自由に行うことができる (free entry) を仮定すると,
$$
V(z) = 0.
$${#eq-free-entry}
よって, @eq-bellman-firm から
$$
\frac{\kappa}{\lambda_{f}(\theta)} = \beta \mathbb{E}[J(z') | z].
$$
直感的には, 求人を出すコスト $\kappa$ はマッチした時の期待値 $\beta \mathbb{E}[J(z') | z]$ とマッチする確率 $\lambda_{f}(\theta)$ の積で決まること解釈できます.
**労働者**
- 無限期間の線形効用を最大化すると考える. 割引率は $\beta$.
- 雇用されている労働者の価値関数を $W(z)$, 失業している労働者の価値関数を $U(z)$ とする
$$
\begin{aligned}
W(z) &= w(z) + \beta \mathbb{E}[(1-\sigma)W(z') + \sigma U(z') | z] \\
U(z) &= b + \beta \mathbb{E}[\lambda_w(\theta)W(z') + (1-\lambda_w(\theta))U(z') | z].
\end{aligned}
$${#eq-bellman-worker}
**賃金交渉**
- マッチした労働者と企業は賃金を交渉すると考える
- 一般ナッシュ交渉を仮定する
$$
\max_{w} \left(\widetilde{W}(w, z) - U(z)\right)^{\gamma}\left(\widetilde{J}(w, z) - V(z)\right)^{1-\gamma}.
$$
ここで, $\widetilde{W}(w, z)$, $\widetilde{J}(w, z)$ は今期の賃金が $w$ の時の労働者と企業の価値関数を表します. そのため, 今までの表現 $W(z), J(z)$ は, 均衡賃金 $w(z)$ をすでに考慮した書き方になっていたということです.
ここで, 一階条件をとると
$$
(1-\gamma)\left(\widetilde{W}(w, z) - U(z)\right) = \gamma \left(\widetilde{J}(w, z) - V(z)\right).
$${#eq-foc-nb}
$U(z)$, $V(z)$ は労働者と企業からみた交渉決裂点 (disagreement point, outside option) であり, それと比べた場合の余剰 (surplus) を交渉力 $\gamma$, $1 - \gamma$ で重み付けて均等化しているということがわかります. もう一つの解釈は, 均衡における総余剰 $\mathcal{S}$ を以下のように定義した時,
$$
\mathcal{S}(z) = \underbrace{W(z) - U(z)}_{\text{Worker Surplus}} + \underbrace{J(z) - V(z)}_{\text{Firm Surplus}},
$$
一階条件 @eq-foc-nb は以下のように書き換えられます.
$$
\begin{aligned}
W(z) &= U(z) + \gamma \mathcal{S}(z), \\
J(z) &= V(z) + (1-\gamma) \mathcal{S}(z).
\end{aligned}
$$
つまり, 労働者と企業は outside option に加えて, 総余剰のそれぞれの交渉力に応じた部分を得ることができるという解釈です.
**均衡**
@eq-bellman-firm, @eq-free-entry, @eq-bellman-worker, @eq-foc-nb によって均衡が定義されます. これらを整理すると, 次の Job Creation Condition (JC) が得られます.
$$
\frac{\kappa}{(1-\gamma)\lambda_{f}(\theta_t)} = \beta \mathbb{E}\left[z_{t+1} - b + \frac{1-\sigma-\gamma\lambda_w(\theta_{t+1})}{1-\gamma}\frac{\kappa}{\lambda_{f}(\theta_{t+1})}\right].
$${#eq-job-creation}
導出は @prp-dmp-eq を参照してください. ここで定常状態を考えると,
$$
\frac{\kappa}{(1-\gamma)\lambda_{f}(\overline{\theta})} = \beta \left(\overline{z} - b + \frac{1-\sigma-\gamma\lambda_w(\overline{\theta})}{1-\gamma}\frac{\kappa}{\lambda_{f}(\overline{\theta})}\right).
$${#eq-ss-jc}
@eq-ss-jc は定常状態の $\overline{\theta} = \frac{\overline{v}}{\overline{u}}$ を定める式とみなすことができます. したがって, 均衡における求人 $v$ と失業率 $u$ の関係は, @eq-beveridge-curve (BC) と @eq-ss-jc (JC) の交点によって決定されます.
::: {#fig-steady-state layout-ncol=2}


Figure 20.5 and 20.6 from @azzimonti2025.
:::
@fig-steady-state の左図は, $BC$ と $JC_1$ の交点によって失業率 $\overline{u}$ と求人 $\overline{v}$ が決定される様子を示しています ($SS_1$).
ここで予期しない恒常的な生産性の低下, $\overline{z}$ が下がったとします. すると @eq-ss-jc から $\overline{\theta}$ が下がり, $JC_1$ から $JC_2$ へシフトします. この時, 移行過程では右図のような変化が起きると考えることができます. 失業率 $u$ はすぐには変化できないため, 求人 $v$ が大きく低下します. その後, 失業率 $u$ が徐々に上昇し, 新しい均衡点 $SS_2$ に到達します.
## Calibration
### Functional Forms
マッチング関数は @eq-matching-cobb-douglas で表されると仮定し, 生産 $z_t$ は以下のように表されるとします.
$$
\hat{z}_{t+1} = \rho \hat{z}_t + \varepsilon_{t+1}
$$
ここで, $\hat{z}_{t}$ は steady state $\overline{z}$ からの log-deviation, つまり
$$
\hat{z}_{t} = \log z_t - \log \overline{z}.
$$
### Parameter Values
モデルのパラメータは先行研究に従い, 以下のように設定します.
::: {#tbl-dmp-params tbl-colwidths="[20, 15, 40]"}
| **Parameter** | **Value** | **Source** |
|:----------------------:|----------:|--------------:|
| $\beta$ | 0.996 | @cooley1995 |
| $\rho$ | 0.949 | @hagedorn2008 |
| $\sigma_{\varepsilon}$ | 0.0065 | @hagedorn2008 |
| $\sigma$ | 0.034 | @shimer2005 |
| $\chi$ | 0.45 | @shimer2005 |
| $b$ | 0.4 | @shimer2005 |
| $\gamma$ | 0.72 | @shimer2005 |
| $\eta$ | 0.72 | @shimer2005 |
Parameter values for the DMP model
:::
- モデルの一期間は1ヶ月とする (@hagedorn2008 では1週間)
- RBCモデルで標準的な1年の割引率 $\beta = 0.947$ [@cooley1995] を1ヶ月に直すと $0.947^{\frac{1}{12}} = 0.996$
- 定常状態において $\overline{z} = 1, \overline{\theta} = 1$ とする
- $\kappa$ の値は定常状態 @eq-ss-jc を用いて次のように計算される
$$
\kappa = \frac{(1-\gamma) \lambda_{f}(\overline{\theta}) \beta (\overline{z} - b)}{1 - \beta (1 - \sigma - \gamma \lambda_{w}(\overline{\theta}))}.
$$
## Simulation
```{julia}
#| label: mdl-dmp
#| code-fold: show
#| output: false
@model DMP begin
κ / ((1 - γ) * λ_f[0]) =
β * (z[1] - b + (1 - σ - γ * λ_w[1]) / (1 - γ) * (κ / λ_f[1]))
λ_f[0] = χ * θ[0]^(-η)
λ_w[0] = χ * θ[0]^(1 - η)
u[0] = (1 - λ_w[-1]) * u[-1] + σ * (1 - u[-1])
v[0] = θ[0] * u[0]
log(z[0]) - log(z̄) = ρ * (log(z[-1]) - log(z̄)) + σ_ε * ε[x]
end
@parameters DMP begin
β = 0.996
ρ = 0.949
σ_ε = 0.0065
σ = 0.034
χ = 0.45
b = 0.4
γ = 0.72
η = 0.72
z̄ = 1.0
θ̄ = 1.0
λ̄_w = χ * θ̄^(1 - η)
κ = (1 - γ) * λ̄_w * β * (z̄ - b) / (1 - β * (1 - σ - γ * λ̄_w))
end
```
```{julia}
#| label: fig-dmp-irf
#| code-fold: true
#| fig-cap: Impulse Response Functions of the DMP Model
plot_irf(DMP, variables=[:u, :v, :z, :θ], periods=100);
```
::: {.content-visible when-format="html"}
```{julia}
#| label: dmp-irf-data
#| include: false
irf = get_irf(DMP, variables=[:u, :v, :z, :θ], periods=100, levels=true)
ss = get_steady_state(DMP)(:, :Steady_state)
u_ss = ss(:u)
v_ss = ss(:v)
z_ss = ss(:z)
θ_ss = ss(:θ)
u_path = [u_ss; collect(irf(:u, :, :ε))]
v_path = [v_ss; collect(irf(:v, :, :ε))]
z_path = [z_ss; collect(irf(:z, :, :ε))]
θ_path = [θ_ss; collect(irf(:θ, :, :ε))]
df_irf = DataFrame(
:t => -1:(length(u_path)-2),
:u => u_path,
:v => v_path,
:z => z_path,
:θ => θ_path,
)
CSV.write(@projectroot("output", "dmp_irf.csv"), df_irf)
# Beveridge Curve
pars = Dict(p[1] => p[2] for p in get_parameters(DMP, values=true))
σ = pars["σ"]
χ = pars["χ"]
η = pars["η"]
u_bc = range(u_ss * (1 - 0.0025), u_ss * (1 + 0.0025), length=100)
v_bc = @. (σ * (1 - u_bc) / (χ * u_bc^η))^(1 / (1 - η))
df_bc = DataFrame(
:u => u_bc,
:v => v_bc
)
CSV.write(@projectroot("output", "dmp_bc.csv"), df_bc)
```
<style>
input[type=range] {
accent-color: #0f6a81;
}
</style>
```{ojs}
//| label: ojs-irf-uv
//| echo: false
irf = FileAttachment("output/dmp_irf.csv").csv({ typed: true })
bc = FileAttachment("output/dmp_bc.csv").csv({ typed: true })
u_ss = irf[0].u
v_ss = irf[0].v
u_min = d3.min(bc, d => d.u)
u_max = d3.max(bc, d => d.u)
v_bc_max = bc.find(d => d.u === u_max).v
theta_max = d3.max(irf, d => d.θ)
dy = (theta_max * u_max - v_ss) * 1.2
jc = irf.flatMap(d => [{t: d.t, u: u_min, v: d.θ * u_min}, {t: d.t, u: u_max, v: d.θ * u_max}])
current_jc_label = irf.map(d => ({t: d.t, u: u_max, v: d.θ * u_max}))
Plot.plot({
style: {fontSize: "16px"},
marginLeft: 70,
marginBottom: 45,
grid: true,
marks: [
Plot.line(bc, {x: "u", y: "v", stroke: "gray", strokeDasharray: "4,4"}),
Plot.text([{u: u_max, v: v_bc_max}], {x: "u", y: "v", text: ["BC"], dy: 20}),
Plot.line(jc, {filter: d => d.t === t, x: "u", y: "v", stroke: "gray", strokeDasharray: "2,2"}),
Plot.text(current_jc_label, {filter: d => d.t === t, x: "u", y: "v", text: d => "JC", dy: -10, dx: -10}),
Plot.line(irf, {filter: d => d.t >= 0 && d.t <= t, x: "u", y: "v", stroke: "#c2676d"}),
Plot.dot(irf, {filter: d => d.t === t, x: "u", y: "v", fill: "#c2676d", r: 5}),
Plot.text(irf, {filter: d => d.t === t, x: "u", y: "v", text: d => `t=${d.t}`, dy: -10}),
Plot.dot([{u: u_ss, v: v_ss}], {x: "u", y: "v", fill: "#0f6a81", r: 5}),
Plot.text([{u: u_ss, v: v_ss}], {x: "u", y: "v", text: ["SS"], dy: 20})
],
x: {label: "Unemployment", domain: [u_min, u_max], labelOffset: 35},
y: {label: "Vacancy", labelOffset: 1, domain: [v_ss - dy, v_ss + dy]}
})
viewof t = Inputs.range([-1, 99], {label: "t =", step: 1, value: -1})
```
:::
### Summary Statistics
![**Summary Statistics for Quarterly U.S. Data from 1951 I to 2004 IV**. [@azzimonti2025, Table 19.2]](/static/img/akmm/chapter19/table2.svg){#tbl-dmp-table2}
```{julia}
#| code-fold: true
#| label: tbl-dmp-stats
#| tbl-cap: Model Statistics
#| tbl-colwidths: [25, 5, 10, 10, 10, 10]
#| output: asis
function sim_one(; burnin, periods, mdl)
sim = get_simulation(mdl, variables=[:u, :v, :z, :θ], periods=periods + burnin, levels=true)
us = sim(:u, burnin+1:burnin+periods, :simulate)
vs = sim(:v, burnin+1:burnin+periods, :simulate)
zs = sim(:z, burnin+1:burnin+periods, :simulate)
θs = sim(:θ, burnin+1:burnin+periods, :simulate)
xs_quarterly = [[mean(xs[i:i+2]) for i in 1:3:length(xs)-3] for xs in (us, vs, θs, zs)]
cycles = [hp_filter(log.(xs), 1600)[1] for xs in xs_quarterly]
std_mdl = [std(xs) for xs in cycles]
acor_mdl = [cor(xs[2:end], xs[1:end-1]) for xs in cycles]
cor_mdl = vcat([cor(cycles[1], cycles[i]) for i in 2:4],
[cor(cycles[2], cycles[i]) for i in 3:4],
[cor(cycles[3], cycles[4])])
df = DataFrame(
pars=["std_u", "std_v", "std_θ", "std_z",
"acor_u", "acor_v", "acor_θ", "acor_z",
"cor_uv", "cor_uθ", "cor_uz", "cor_vθ", "cor_vz", "cor_θz"],
value=vcat(std_mdl, acor_mdl, cor_mdl))
end
function get_table(; n_sim=1000, burnin=100, periods=648, mdl=DMP)
df = sim_one(burnin=burnin, periods=periods, mdl=mdl)
for i in 2:n_sim
df_i = sim_one(burnin=burnin, periods=periods, mdl=mdl)
df = vcat(df, df_i)
end
res = combine(groupby(df, :pars),
[:value] .=> mean .=> [:value]
)[!, :value]
tb = DataFrame(
desc=["Standard Deviation", "Quartely Autocorrelation", missing,
"Correlation Matrix", missing, missing],
tmp=["", "", "\$u\$", "\$v\$", "\$v/u\$", "\$z\$"],
u=[res[1], res[5], 1, missing, missing, missing],
v=[res[2], res[6], res[9], 1, missing, missing],
θ=[res[3], res[7], res[10], res[12], 1, missing],
z=[res[4], res[8], res[11], res[13], res[14], 1]
)
return tb
end
df_mdl = get_table()
pretty_table(df_mdl, backend=:markdown, allow_markdown_in_cells=true,
alignment=[:l, :c, :r, :r, :r, :r],
column_labels=["", "", "\$u\$", "\$v\$", "\$v/u\$", "\$z\$"],
formatters=[
(v, i, j) -> ismissing(v) ? "" : v,
(v, i, j) -> v isa Number ? @sprintf("%.3f", v) : v
]
)
```
@tbl-dmp-stats はシミュレーションの結果を示しています. @tbl-dmp-table2 と比較すると, 各パラメータの相関はおおむね一致しています. しかし, $u, v, \theta = v/u$ の標準偏差が実際のデータよりも小さくなっていることがわかります. この点は, DMPモデルの重要な課題の一つとして知られており, "Labor Market Volatility Puzzle", あるいは Shimer Puzzle [@shimer2005] と呼ばれます.
## RBC meets DMP
ここからは, RBCモデルにDMPフレームワークを組み込んだモデルを考えます. 次の3つが大きな違いです.
1. 凹型の効用関数
1. 生産関数に資本を導入
1. 企業の利潤を所有者に帰属^[今までは企業はこの経済の外部から所有されていると暗に仮定していました.]
### 設定
- 消費者は $(i, j) \in [0, 1]^2$ のユニットスクエアに分布している
- $i$ は家族を表し, $j$ は家族内の個人を表す. 家族のメンバーは同一であると考える
- 家族 $i$ は互いに同一であると考える. したがって, 代表的家族 (representative family) を考えることができる
- 家族内の所得はプールされ, 消費は均等に分配されると考える. したがって, 世帯主 (household head) の効用を最大化することを考える
**家計**
代表的家計の世帯主の問題を考えるため, $i, j$ を省略します.
$$
\max_{\{c_t\}} \mathbb{E}_0 \sum_{t=0}^{\infty} \beta^t \mathcal{U}(c_t)
$$
subject to
$$
c_t + k_{t+1} = (1+r_t - \delta) k_t + (1-u_t) w_t + u_t b + d_t
$$
- $u_t$: 失業率. 家族の中にいる失業者の割合
- $b$: 失業給付 (unemployment benefit) または home production
- $d_t$: 企業からの配当 (dividend)
**企業**
代表的企業の生産関数は次のコブ・ダグラス型とします.
$$
Y_t = z_t K_t^{1-\alpha} N_t^{\alpha}.
$$
なお, 労働投入量は雇用数と一致するため $N_t = 1 - u_t$ です. ここで, 労働者一人あたりの資本投入量を $k_{f, t} := \frac{K_t}{1-u_t}$ とすると, 企業の最適資本量選択問題は次のように表されます.
$$
\max_{k_{f, t}} z_t k_{f, t}^{\alpha} - r_t k_{f, t}
$$
一階条件より $r_t = \alpha z_t k_{f, t}^{\alpha - 1}$ となり, 均衡における資本価格は次のように表されます.
$$
r(z_t, K_t, u_t) = \alpha z_t \left(\frac{K_t}{1-u_t}\right)^{\alpha - 1}.
$$
ここで, 状態変数を $X_t := (z_t, K_t, u_t)$ と定義し, マッチごとの企業余剰を $y(X_t)$ と表すと,
$$
\begin{aligned}
y(X_t) &= z_t \left(\frac{K_t}{1-u_t}\right)^{\alpha} - r(X_t) \frac{K_t}{1-u_t} \\
&= (1-\alpha) z_t \left(\frac{K_t}{1-u_t}\right)^{\alpha}.
\end{aligned}
$$
### ベルマン方程式
**家計**
$$
\mathcal{V}(k, X) = \max_{c, k'} \mathcal{U}(c) + \beta \mathbb{E}\left[\mathcal{V}(k', X') | z\right]
$$
subject to
$$
\begin{aligned}
c + k' &= (1 + r(X) - \delta) k + (1-u) w(X) + u b + d(X), \\
K' &= \Omega(X), \\
u' &= (1 - \lambda_w(\theta(X))) + \sigma (1 - u).
\end{aligned}
$$
ここで $\Omega(X)$ は資本蓄積の法則 (Law of motion of capital) を表します. また, $w(X), d(X)$ はそれぞれ均衡賃金と企業の配当を表します. ここから, 状態価格 (state price) が導けます.
$$
Q(z', X) = \beta f(z' | z) \frac{\mathcal{U}_c(C(z', \Omega(X), u'(X)))}{\mathcal{U}_c(C(X))}
$$
ここで, $f(z' | z)$ は状態 $z$ から次期の状態 $z'$ への遷移確率密度関数を表します. $Q(z', X)$ の解釈としては
- 次の期に $z'$ が実現した時に, 1単位の消費をもらえる保険 (Arrow security) の価格
- 各状態 $z'$ に対する確率的割引因子
この状態価格を導入すると, 労働者や企業の価値関数が $Q(z', X)$ を用いた形でかけます. それぞれの導出は @azzimonti2025 の Chapter 20 とその付録を参照してください.
**労働者**
家族にとって, 家族のメンバー (労働者) は, 確率的に雇用状態の変化する所得の過程とみなすことができます. したがって, 労働者の価値関数は $Q(z', X)$ を用いて次のように表されます.
$$
\begin{aligned}
W(X) &= w(X) + \int Q(z', X)\left((1-\sigma)W(X') + \sigma U(X')\right)\, dz' \\
U(X) &= b + \int Q(z', X)\left(\lambda_w(\theta(X))W(X') + (1-\lambda_w(\theta(X)))U(X')\right)\, dz'
\end{aligned}
$${#eq-bellman-worker-dmp-rbc}
導出の詳細は @azzimonti2025 の付録20.A.6 を参照してください.
**企業**
企業の価値関数も同様にして次のように表されます.
$$
\begin{aligned}
J(X) &= y(X) - w(X) + \int Q(z', X)\left((1-\sigma)J(X') + \sigma V(X')\right)\, dz' \\
V(X) &= -\kappa + \int Q(z', X)\left((1-\lambda_f(\theta(X)))V(X') + \lambda_f(\theta(X)) J(X')\right)\, dz'
\end{aligned}
$${#eq-bellman-firm-dmp-rbc}
導出の詳細は @azzimonti2025 の付録20.A.6 を参照してください. また, Free entry condition $V(X) = 0$ から,
$$
\frac{\kappa}{\lambda_f(\theta(X))} = \int Q(z', X) J(X')\, dz'.
$${#eq-free-entry-dmp-rbc}
### Equilibrium Conditions
**Job Creation Condition**
@eq-bellman-worker-dmp-rbc, @eq-bellman-firm-dmp-rbc, @eq-free-entry-dmp-rbc から, @prp-dmp-eq と同様にして, Job Creation Condition が導出されます.
$$
\frac{\kappa}{(1-\gamma)\lambda_{f}(\theta(X))} = \int Q(z', X) \left[y(X') - b + \frac{1-\sigma-\gamma\lambda_w(\theta(X'))}{1-\gamma}\frac{\kappa}{\lambda_{f}(\theta(X'))}\right]\, dz'.
$${#eq-job-creation-dmp-rbc}
**Euler Equation**
標準的なRBCモデルであるため, 家計の最適化条件から Euler Equation が導出されます.
$$
1 = \int Q(z', X) (1 + r(X') - \delta)\, dz'.
$$
**Resource Constraint**
$$
K' = (1 - \delta) K + Y - C - \kappa v
$$
- Vacancy cost $\kappa v$ は財で支払われると仮定
- 人口が1であるため, 総消費 $C$ は一人当たり消費 $c$ と一致
<!-- The result does not match the ones in Azzimonti et al. (2025)
### Calibration
@tbl-dmp-params に加えて, 以下のパラメータを設定します.
::: {#tbl-dmp-params-rbc tbl-colwidths="[20, 15, 40]"}
| **Parameter** | **Value** | **Source** |
|:----------------------:|----------:|--------------:|
| $\beta$ | 0.996 | @cooley1995 |
| $\alpha$ | 0.4 | @cooley1995 |
| $\delta$ | 0.004 | @cooley1995 |
Parameter values for the RBC+DMP model
:::
また, 効用関数は $\mathcal{U}(c) = \log (c)$ とします. 元々のDMPモデルと一つ異なるのは, 失業給付 $b$ の値を $y(X)$ の定常状態の値 $\overline{y}$ の40% であると定める点です.
### Simulation
```{julia}
#| label: mdl-dmp-rbc
#| code-fold: show
#| output: false
@model RBC_DMP begin
# Matching
λ_f[0] = χ * θ[0]^(-η)
λ_w[0] = χ * θ[0]^(1 - η)
u[0] = (1 - λ_w[-1]) * u[-1] + σ * (1 - u[-1])
v[0] = θ[0] * u[0]
N[0] = 1 - u[0]
# Firm side
k_f[0] = K[0] / N[0]
r[0] = α * z[0] * k_f[0]^(α - 1)
y[0] = (1 - α) * z[0] * k_f[0]^α
Y[0] = z[0] * K[0]^α * N[0]^(1 - α)
# Euler equation
1 = β * (C[0] / C[1]) * (1 + r[1] - δ)
# Job creation condition
κ / ((1 - γ) * λ_f[0]) = β * (C[0] / C[1]) * (y[1] - b + (1 - σ - γ * λ_w[1]) / (1 - γ) * (κ / λ_f[1]))
# Resource constraint
I[0] = K[0] - (1 - δ) * K[-1]
Y[0] = C[0] + I[0] + κ * v[0]
# Productivity shock
log(z[0]) - log(z̄) = ρ * (log(z[-1]) - log(z̄)) + σ_ε * ε[x]
end
@parameters RBC_DMP begin
# RBC parameters
β = 0.996
α = 0.4
δ = 0.004
# DMP parameters
ρ = 0.949
σ_ε = 0.0065
σ = 0.034
χ = 0.45
γ = 0.72
η = 0.72
# Steady state values
z̄ = 1.0
θ̄ = 1.0
λ̄_w = χ * θ̄^(1 - η)
λ̄_f = χ * θ̄^(-η)
r̄ = 1 / β - 1 + δ
k̄_f = (r̄ / (α * z̄))^(1 / (α - 1))
ȳ = (1 - α) * z̄ * k̄_f^α
# Calibration of b and κ
b = 0.4 * ȳ
κ = λ̄_f * (β * (1 - γ) * (ȳ - b)) / (1 - β * (1 - σ - γ * λ̄_w))
end
```
```{julia}
#| label: irf-dmp-rbc
#| code-fold: true
plot_irf(RBC_DMP; periods=200, variables=[:z, :u, :θ, :v]);
```
```{julia}
plot_irf(RBC_DMP; periods=200, variables=[:N, :Y, :C, :I]);
```
```{julia}
#| label: tbl-dmp-rbc-stats
#| code-fold: true
#| tbl-cap: "Model Statistics for RBC+DMP Model: Labor Market"
#| tbl-colwidths: [25, 5, 10, 10, 10, 10]
#| output: asis
df_mdl = get_table(mdl=RBC_DMP)
pretty_table(df_mdl, backend=:markdown, allow_markdown_in_cells=true,
alignment=[:l, :c, :r, :r, :r, :r],
column_labels=["", "", "\$u\$", "\$v\$", "\$v/u\$", "\$z\$"],
formatters=[
(v, i, j) -> ismissing(v) ? "" : v,
(v, i, j) -> v isa Number ? @sprintf("%.3f", v) : v
]
)
```
-->