---
engine: julia
---
# Real Business Cycle Model {#sec-rbc}
```{julia}
#| label: setup-rbc
#| output: false
#| code-fold: true
using ProjectRoot
using PrettyTables
using Printf
using DataFrames
using CSV
using LaTeXStrings
using QuantEcon: hp_filter
using Dates
using Statistics
using StatsPlots
using MacroModelling: @model, @parameters, get_simulation,
get_irf, plot_irf, plot_simulation, get_steady_state
import Random
Random.seed!(1234)
mypalette = ["#d5968c", "#c2676d", "#5c363a", "#995041", "#45939c", "#0f6a81"]
default(size=(600, 370), titlefontsize=10, fmt=:svg, grid=false,
foreground_color_legend=nothing, palette=mypalette[[6, 2, 4, 3, 1, 5]])
```
## Real Business Cycle (RBC) Model とは
Real Business Cycle (RBC) モデルとは, 経済のビジネスサイクルを説明するためのマクロ経済学のモデルです. RBCモデルは, 経済の変動が主に技術的な要因や生産性の変化によって引き起こされると仮定しています.
- **Real**: 貨幣や他の名目変数を考慮しない
- **Business Cycle**: 長期的なトレンド (成長) と短期的な変動を考慮する
これまで学んだRamseyモデルでも, 貨幣や名目変数を考慮しない, つまりRealなモデルでした. また, Ramseyモデルでも, 生産性 (TFP) の成長を考慮していました. RBCモデルでは, TFPの成長を確率的なもの (stochastic) なものとして考えます. まとめると以下のようになります.
$$
\text{RBC Model} = \text{Ramsey Model} + \text{Stochastic TFP}.
$$
RBCモデルへの主要な貢献に対してKydlandとPrescottが2004年にノーベル経済学賞を受賞しています (@fig-nobel-2004).
](/static/img/01-rbc/nobel2004.png){fig-align="center" width="60%" #fig-nobel-2004}
## Stylized Facts {#sec-facts}
### トレンドとサイクル
@lucas1977 や @kydland1982 は景気循環を**トレンド**と**サイクル**に分けて考えることを提案しました. トレンドは長期的な成長を表し, サイクルは短期的な変動を表します.
{#fig-business-cycle width="90%" fig-align="center"}
@fig-business-cycle のように景気循環とは, 成長トレンドの周りにPeakとTroughを持つ波のような動きととらえます. 特に, PeakからTroughまでの期間を**不景気** (recession) と呼び, TroughからPeakまでの期間を**好景気** (boom, expansion) と呼びます.
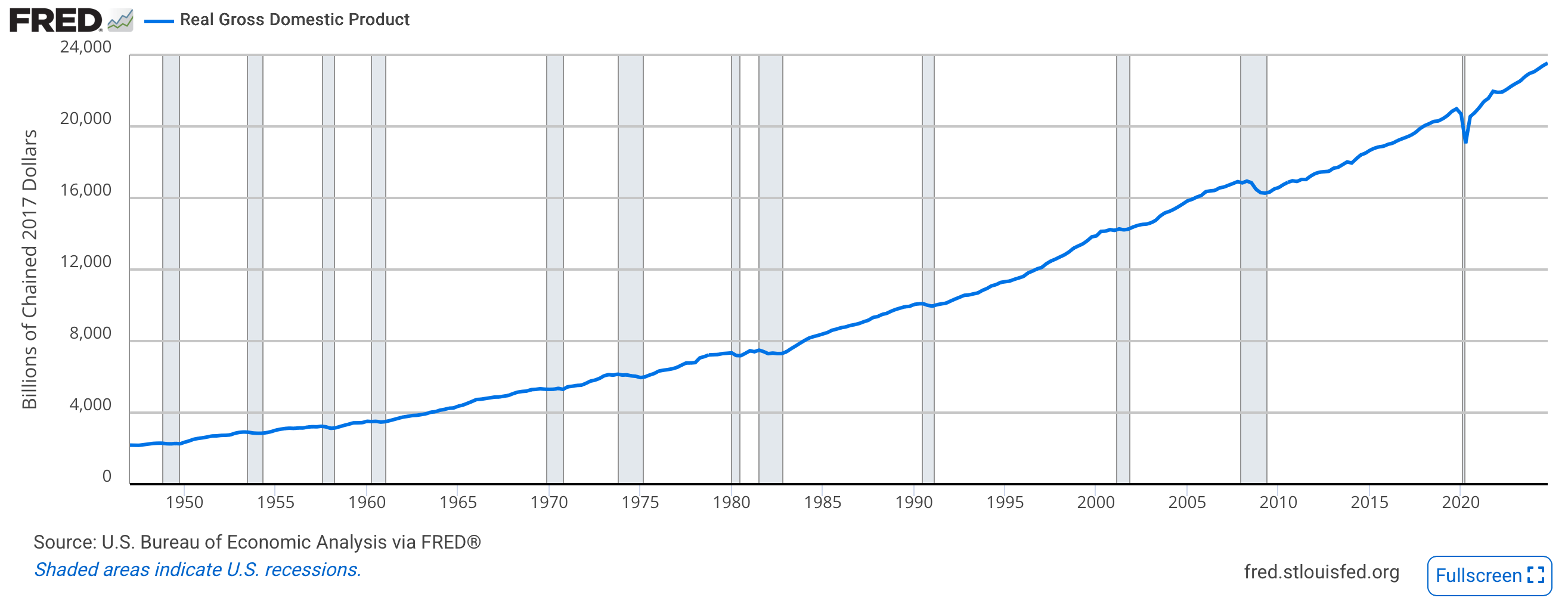
.](/static/img/01-rbc/fred_rgdp.png){#fig-us-rgdp}
例えば, アメリカの実質GDPの時系列データを見てみましょう (@fig-us-rgdp). アメリカの実質GDPは成長傾向をもちながらも短期的な変動を繰り返しています. 特にグレーの部分は不景気を示しており, National Bureau of Economic Research (NBER) の Business Cycle Dating Committee が様々な経済指標を用いて, アメリカが不景気にあるかを定義しています.
### Hodrick and Prescott Filter
Hodrick-Prescott (HP) フィルターは, 時系列データからトレンド成分とサイクル成分を分離するための手法です.
::: callout-note
## Hodrick and Prescott Filter
時系列データ $\{Y\}_{t=0}^T$ に対して, HPフィルターは以下の最適化問題を解くことでトレンド成分 $\{\tau_t\}$ を求める.
$$
\min_{\{\tau_t\}} \sum_{t=1}^{T} \left(Y_t - \tau_t\right)^2 +
\lambda \left[\sum_{t=2}^{T-1} \left((\tau_{t+1} - \tau_t) - (\tau_t - \tau_{t-1})\right)^2\right]
$${#eq-hp-filter}
ここで平滑化パラメータ $\lambda$ は四半期データなら $1600$, 年次データなら $100$ が一般的に用いられる.
:::
直感的にはある程度スムーズなトレンド成分を求めるために, トレンド成分の符号の反転に大きくペナルティを欠けているというイメージです. @fig-hp-penalized を見ると, 符号が反転するような $\tau_t$ の取り方はペナルティが大きくなり, そのような $\tau_t$ が選ばれにくいことがわかります.
{width="80%" fig-align="center" #fig-hp-penalized}
一方で, @fig-hp-smooth は, 符号が反転しにくい $\tau_t$ の取り方はペナルティが小さくなり, そのような $\tau_t$ が選ばれやすいことを示しています. 今回の例では, $y_t$ が上昇傾向にあるように見えるので, 一定のペースで上昇するような $\tau_t$ が選ばれやすくなっています.
{width="80%" fig-align="center" #fig-hp-smooth}
この異符号に対する大きなペナルティは, @eq-hp-filter のペナルティ項を展開して見ると違いがよく分かります.
$$
\begin{aligned}
&\sum_{t=2}^{T-1} \left((\tau_{t+1} - \tau_t) - (\tau_t - \tau_{t-1})\right)^2 \\
&= \sum_{t=2}^{T-1} (\tau_{t+1} - \tau_t)^2 + \sum_{t=2}^{T-1} (\tau_t - \tau_{t-1})^2 - 2\sum_{t=2}^{T-1} (\tau_{t+1} - \tau_t)(\tau_t - \tau_{t-1}) \\
&= \underbrace{(\tau_{T} - \tau_{T-1})^2 + 2\sum_{t=2}^{T-1} (\tau_t - \tau_{t-1})^2}_{\text{Penalty for large difference}} \underbrace{- 2\sum_{t=2}^{T-1} (\tau_{t+1} - \tau_t)(\tau_t - \tau_{t-1})}_{\text{Penalty for sign change}}.
\end{aligned}
$$
最初の項は, トレンド成分の変化が大きい場合にペナルティを課すものであり, 2番目の項はトレンド成分の符号が反転する場合にペナルティを課すものです. そのため, 符号が反転しにくいようなトレンド成分が選ばれやすくなります.
**HP Filter の実践**
@fig-hp-filter は, アメリカの実質GDPの時系列データにHPフィルターを適用した結果です. Juliaでは, `QuantEcon.hp_filter` 関数を用いてHPフィルターを適用できます.
```{julia}
#| label: fig-hp-filter
#| fig-cap: "**Data and Trend of Logs of U.S. Aggregates.** Quartely Data 1948I-2025III from FRED. HP filter with $\\lambda = 1600$."
#| code-fold: true
data = CSV.read(@projectroot("data", "fred_data.csv"), DataFrame; missingstring="NA")
function plot_trend(var, title; data=data, λ=1600, legend=false)
xs = log.(data[!, var])
cycle, trend = hp_filter(xs, λ)
years = unique(year.(data.date))
year_ticks = [Date(y, 1, 1) for y in years[1:15:end]]
year_labels = [string(y) for y in years[1:15:end]]
p = plot(data.date, trend, label="HP trend", title=title, legend=legend,
xticks=(year_ticks, year_labels))
plot!(p, data.date, xs, label="Data")
return p
end
p1 = plot_trend("gdp", "Real GDP", legend=:topleft)
p2 = plot_trend("consumption", "Consumption")
p3 = plot_trend("labor", "Labor Hours")
p4 = plot_trend("investment", "Investment")
plot(p1, p2, p3, p4, layout=(2, 2))
```
```{julia}
#| label: fig-hp-cycle
#| fig-cap: "GDP Cycle and Other Cycles. Data from FRED. HP filter with $\\lambda = 1600$."
#| code-fold: true
function plot_cycle(var, title; data=data, λ=1600, legend=false)
xs = log.(data[!, var])
cycle, trend = hp_filter(xs, λ)
years = unique(year.(data.date))
year_ticks = [Date(y, 1, 1) for y in years[1:15:end]]
year_labels = [string(y) for y in years[1:15:end]]
p = plot(data.date, cycle, label=false, title=title, legend=legend,
xticks=(year_ticks, year_labels))
cycle_gdp, _ = hp_filter(log.(data[!, "gdp"]), λ)
plot!(p, data.date, cycle_gdp, label="GDP cycle")
return p
end
p1 = plot_cycle("gdp", "Real GDP", legend=:bottomleft)
p2 = plot_cycle("consumption", "Consumption")
p3 = plot_cycle("labor", "Labor Hours")
p4 = plot_cycle("investment", "Investment")
plot(p1, p2, p3, p4, layout=(2, 2))
```
@fig-hp-cycle は, Real GDP のサイクル成分と他の経済変数のサイクル成分を比較したものです. これを見ると消費と労働時間のサイクル成分はGDPのサイクル成分と似た動きをしていることがわかります. 一方で, 投資のサイクル成分はGDPのサイクル成分よりも変動が大きいことがわかります.
なお, HPフィルターは慣例的に用いられている手法ですが
1. $\lambda$ の選び方によって結果が変わる
2. HPフィルターの関数形に経済学的な裏付けがない
などの問題点があるため, Band Pass Filter [@baxter1999] など他の手法も検討されています.
### 景気循環統計
RBCモデルの研究では, 景気循環の特徴を定量的に評価するために, 2次モーメントを計算します. 具体的には, 各経済変数の標準偏差, 自己相関係数, 相関係数を計算します. (1次モーメントである平均は, トレンド成分を除去した後はゼロになるため, 特に計算する必要はありません.) ここでは時系列データに対して, 対数をとりHPフィルターを適用した後に, 各経済変数の2次モーメントを計算します.
```{julia}
#| code-fold: true
#| label: tbl-stats-data
#| tbl-cap: Business Cycle Statistics from U.S. Data 1948I-2025II.
#| output: asis
λ = 1600
gdp_cycle, _ = hp_filter(log.(data[!, "gdp"]), λ)
cons_cycle, _ = hp_filter(log.(data[!, "consumption"]), λ)
inv_cycle, _ = hp_filter(log.(data[!, "investment"]), λ)
labor_cycle, _ = hp_filter(log.(data[!, "labor"]), λ)
cycles = [gdp_cycle, cons_cycle, inv_cycle, labor_cycle]
df_data = DataFrame(
pars=["GDP", "Consumption", "Investment", "Labor Hours"],
std=100 .* std.(cycles),
std_rel=std.(cycles) ./ std(gdp_cycle),
acor=[cor(cycle[begin:end-1], cycle[begin+1:end]) for cycle in cycles],
cory=[cor(gdp_cycle, cycle) for cycle in cycles]
)
pretty_table(
df_data,
alignment=[:l, :r, :r, :r, :r],
column_labels=["Variable", "Std. Dev. (%)", "SD rel. to GDP",
"Autocorrelation", "Corr. with GDP"],
backend=:markdown,
allow_markdown_in_cells=true,
formatters=[(v, i, j) -> v isa Number ? @sprintf("%.3f", v) : v]
)
```
## Model
### 設定
- 経済は一人の代表的消費者からなる
- 効用 $U(c, l)$ は消費 $c$ と余暇 $l$ の関数
- 消費者は一単位の時間をもち, 労働 $n$ と余暇 $l$ を選択する ($n + l = 1$)
- 離散時間を仮定し, 期待効用最大化問題を解く
$$
\mathbb{E}_0 \sum_{t=0}^{\infty} \beta^t U(c_t, l_t).
$$
**生産関数**
- $Y_{t} = z_t F(k_t, n_t)$
- $z_t$ は生産性 (TFP) であり以下のAR(1)過程に従う (詳細は @sec-ar1-process)
$$
\log z_t = \rho_z \log z_{t-1} + \sigma_z \varepsilon_t, \quad \varepsilon_t \sim N(0, 1).
$$
**資本蓄積**
$$
k_{t+1} = (1-\delta) k_t + i_t
$${#eq-capital-accumulation}
- $k_t$ は資本ストック, $i_t$ は投資, $\delta$ は減耗率
**予算制約**
$$
c_t + i_t = z_t F(k_t, n_t).
$$
### ベルマン方程式
上記の生産関数, 資本蓄積, 予算制約を元の効用最大化問題に組み込むと, 以下の問題が導けます.
$$
V(k_0, z_0) = \max_{\{k_{t+1}(z_t), n_t(z_t)\}_{t=0}^{\infty}} \mathbb{E}_0 \sum_{t=0}^{\infty} \beta^t U(z_tF(k_t, n_t) + (1-\delta)k_t - k_{t+1}, 1 - n_t).
$$
ここで, $t=0$ の時点では, $k_0$ と $z_0$ が与えられています. また, $k_{t+1}, n_{t}$ が $z_t$ の実現値に依存していることに注意してください. $t=0$ 時点で決定している変数に着目すると
$$
\begin{aligned}
&V(k_0, z_0) = \max_{k_1, n_0} U(z_0F(k_0, n_0) + (1-\delta)k_0 - k_1, 1 - n_0) \\
&+ \beta \mathbb{E}_{z_1}\left[
\underbrace{\max_{\{k_{t+2}(z_{t+1}), n_{t+1}(z_{t+1})\}_{t=0}^{\infty}} \mathbb{E}_1 \sum_{t=0}^{\infty} \beta^{t} U(z_{t+1}F(k_{t+1}, 1 - n_{t+1}) + (1-\delta)k_{t+1} - k_{t+2}, 1 - n_{t+1})}_{V(k_1, z_1)}\middle| z_0 \right].
\end{aligned}
$$
ここで $t=0$ の時点では $z_1$ の実現値は分からず, 期待値をとっている点に注意してください. これをまとめると以下のようなベルマン方程式が得られます.
$$
V(k, z) = \max_{k', n} U\left(zF(k, n) + (1-\delta)k - k', 1-n\right) + \beta \mathbb{E}[V(k', z') | z].
$$
**最適条件**
価値関数 $V(k, z)$ の微分可能性を仮定し, 効用最大化問題の一階条件を求める. $k'$ に関する一階条件は
$$
U_1(c, 1 - n) = \beta \mathbb{E}[V_{1}(k', z') | z].
$$ {#eq-foc-kprime}
$n$ に関する一階条件は
$$
z F_{2}(k, n) = \frac{U_{2}(c, 1 - n)}{U_{1}(c, 1 - n)}.
$$ {#eq-foc-n}
$k$ に関する Envelope 条件を求めると
$$
V_{1}(k, z) = (zF_{1}(k, n) + 1-\delta) U_1(c, 1 - n).
$$ {#eq-envelope}
ここで, @eq-foc-kprime と @eq-envelope から,
$$
U_{1}(c, 1 - n) = \beta \mathbb{E}[(z F_{1}(k', n') + 1 - \delta)U_{1}(c', 1 - n') | z].
$$ {#eq-euler}
**Intratemporal and Intertemporal Optimal Conditions**
@eq-foc-n と @eq-euler の2本の式がRBCモデルを特徴づける式です. @eq-foc-n は同時点 (Intratemporal) での最適条件, @eq-euler は異時点 (Intertemporal) での最適条件を表し, オイラー方程式とも呼ばれます.
- @eq-foc-n は消費と余暇の間の限界代替率 (MRS) が労働の限界生産性 (MPL) に等しいことを示しています
- @eq-euler は, 消費の限界効用が, 将来の消費の限界効用の期待値と割引率の積に等しいことを示しています
## Calibration
### RBCモデルにおける標準的なパラメータ
RBCモデルの研究では, 以下のパラメータが慣例的に用いられます. その多くを @kydland1982, @prescott1986 または @cooley1995 から引用しています.
::: {#tbl-rbc-parameters tbl-colwidths="[15, 30, 20, 35]"}
| **Parameter** | **Description** | **@prescott1986** | **@cooley1995** |
|:-------------:|:------------------------|------------------:|----------------:|
| $\beta$ | 割引率 | 0.99 | 0.987 |
| $\sigma$ | 効用関数の曲率 | 1.0 | 1.0 |
| $\phi$ | 効用関数の余暇の重み | 0.66 | 0.64 |
| $\alpha$ | 資本のシェア | 0.36 | 0.4 |
| $\delta$ | 資本の減耗率 | 0.025 | 0.012 |
| $\rho_z$ | TFPの自己回帰係数 | 0.9 | 0.95 |
| $\sigma_z$ | TFPのショックの標準偏差 | 0.007 | 0.007 |
Standard RBC model parameters. Quarterly frequency.
:::
なお, @prescott1986 は年率であるため, 四半期率への変換は以下のように行なっています.
- $\beta_{\text{quarter}} = \beta_{\text{year}}^{\frac{1}{4}} = 0.96^{\frac{1}{4}} \approx 0.99$
- $\delta_{\text{quarter}} = 1 - (1 - \delta_{\text{year}})^{\frac{1}{4}} = 1 - (1 - 0.1)^{\frac{1}{4}} \approx 0.025$
注意しなければならないのは, これらの数字は当時のアメリカ経済に基づいているため, 異なる国や時代では異なる値を取る可能性があるということです.
### 標準的なパラメータの導出
RBCモデルやその派生となるモデルも上記のパラメータ値が使われることが多いですが, これらのパラメータの導出方法を知っておくことは重要です.
**資本分配率** $\alpha$
Cobb-Douglas型の生産関数を仮定した時の, 労働分配率 (Labor share) $\frac{wN}{Y}$ は $1-\alpha$ と表せます. これは, 均衡において, 労働の限界生産性 (MPL) が賃金 (wage) に等しいことから導かれます.
$$
w = \frac{\partial Y}{\partial N} = (1 - \alpha) \frac{Y}{N}.
$$
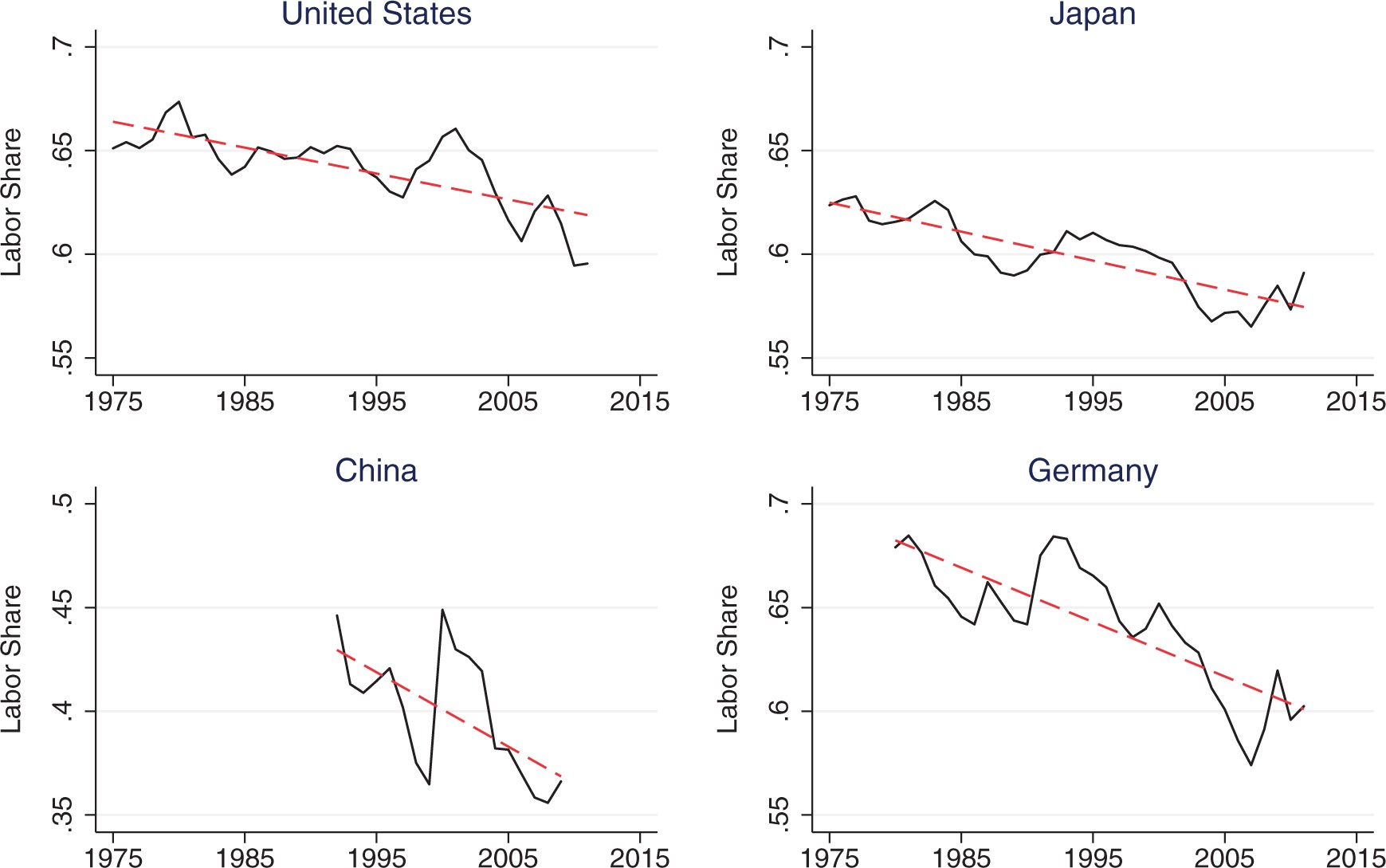
{#fig-labor-share width="80%"}
@fig-labor-share を見ると, アメリカでは2000年までは労働分配率はおおむね 0.64 であったことがわかります. そのため, @prescott1986 のように資本分配率は $0.36$ と導けます. ただし, グラフからも分かるように近年は労働分配率が減少しているため, この仮定を使うことは難しくなってきています.
**資本の減耗率** $\delta$
資本減耗率は @kydland1982 のモデルにおける定常状態から推定した年率 $0.1$ (四半期換算で0.025) が用いられることが多いです. @kydland1982 のモデルは今回紹介したモデルと少し異なるため, @cooley1995 の方法を紹介します.
@cooley1995 のモデルでは, 生産関数に外生的な成長率 $\gamma$ を導入しています. @eq-capital-accumulation を $y_t$ で割ると,
$$
\frac{y_{t+1}}{y_t}\frac{k_{t+1}}{y_{t+1}} = (1-\delta) \frac{k_t}{y_t} + \frac{i_t}{y_t} \Rightarrow
(1+\gamma) \frac{k_{t+1}}{y_{t+1}} = (1-\delta) \frac{k_t}{y_t} + \frac{i_t}{y_t}
$$
定常状態では,
$$
(1+\gamma) \frac{k}{y} = (1-\delta) \frac{k}{y} + \frac{i}{y} \Rightarrow \frac{i}{k} = (\gamma + \delta).
$$
長期の投資資本比率 $\frac{i}{k} = 0.076$^[これの詳細はかなり複雑そうなので省略します.], 成長率 $\gamma = 0.028$ を用いて, $\delta = 0.048$ (年率) を導出できます. 四半期換算すると, $\delta = 0.012$ です. @fig-gmd-growth は, アメリカの実質GDPの成長率であり $\gamma = 0.028$ がおおむね妥当な値であることが分かります.
```{julia}
#| label: fig-gmd-growth
#| code-fold: true
#| fig-cap: "**Growth Rate of Real GDP in the US.** Data from @mueller2025."
gmd = CSV.read(@projectroot("data", "gmd_data.csv"), DataFrame; missingstring="NA")
data_filtered = filter(row -> row.year >= 1950, gmd)
plot(data_filtered.year, data_filtered.rate_growth, label=false, size=(500, 309),
ylabel="Growth Rate (%)")
```
**効用関数の曲率 (Curvature)** $\sigma$
戦後のアメリカでは以下の現象が見られました.
- 実質賃金は一定割合で上昇している (Balanced growth path)
- 消費も一定割合で上昇している
- 労働時間はおおむね一定である
@king1988 はBalanced growth path と労働時間一定を仮定した場合, 効用関数の形状は以下のように制約されることを示しました. (KPR型効用関数)
$$
u(c, l) = \frac{(c v(l))^{1-\sigma} - 1}{1 - \sigma}.
$$
ここで, $v(\cdot)$ は strictly increasing, strictly concave, $v'(0) = -\infty$ を満たす関数です. $\sigma$ の値に関しては多くの先行研究がありますが, 一般に決定するのは難しいです. ここでは最も単純な形として $\sigma = 1$ を仮定し, $v(l) = l^{\frac{\phi}{1-\phi}}, 0 < \phi < 1$ を仮定します. これにより, 効用関数は以下のようになります.[^01-rbc-1]
[^01-rbc-1]: Prescott の主張する消費と余暇の代替弾力性がおおよそ1であるという点も満たしている.
$$
u(c, l) = (1-\phi) \log c + \phi \log l.
$$ {#eq-utility}
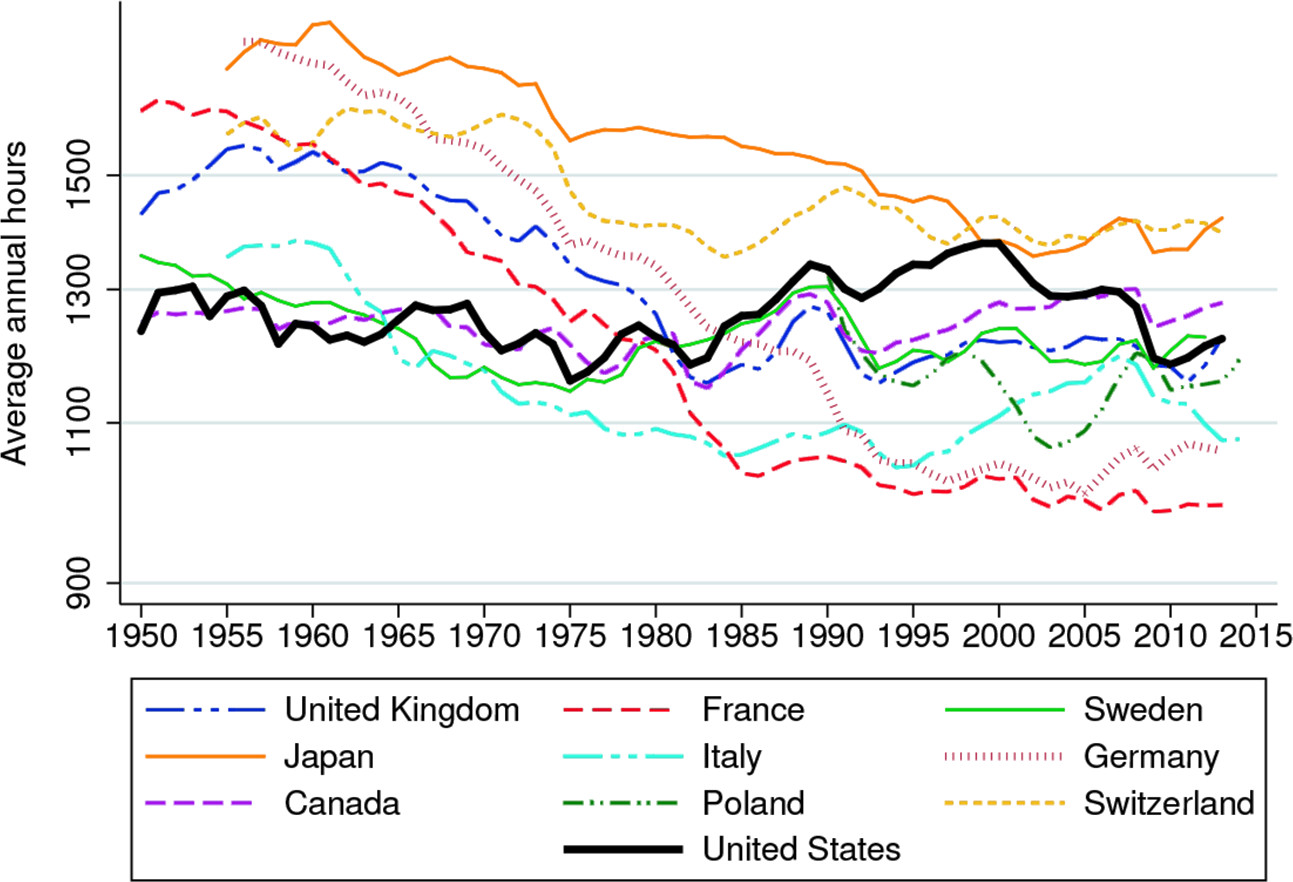
なお, 労働時間が一定であるという点は近年の研究では問題視されています. @boppart2020 は, balanced growth path 上で, 労働時間が減少することを許容した効用関数を提案しています.
{#fig-boppart2020-fig3 width="80%"}
> "The absence of a trend in hours worked in the postwar United States is an exception."
> --- @boppart2020
**効用関数の余暇の重み** $\phi$
このパラメータの推定値は研究によってブレがあります. 以下では簡単な数値例を示します.
@eq-utility を @eq-foc-n に代入することで, 以下の式が導けます.
$$
\frac{\phi}{1-\phi}\frac{n_t}{1-n_t} = (1-\alpha)\frac{y_t}{c_t}
$$
- 1日に8時間労働をするとして, $n_t = \frac{8}{24} = \frac{1}{3}$.
- 最も単純な形の労働分配率として $1 - \alpha = \frac{2}{3}$
- GDPに締める消費の割合 (BGP上では定数) として, $\frac{c_t}{y_t} = \frac{3}{4}$
- @cooley1995 の値に近い
- @fig-ratio-cons-gdp と比べるとやや小さい値である.^[
ここでは簡易的にGDPに対する個人消費の割合を示していますが, 政府支出も民間に還元されていると考えられるため, 政府消費も含める必要があります. また, @cooley1995 では民間の耐久財消費を投資として扱うなど, モデル上の定義に合わせるために, 細かい調整が行われています.
]
これらを計算すると, $\phi = \frac{16}{25} = 0.64$ が得られ, おおむね @prescott1986 や @cooley1995 の値と一致します. ここでは, @azzimonti2025 の推定結果である $\phi = 0.6325$ を用います.
```{julia}
#| label: fig-ratio-cons-gdp
#| fig-cap: "**Share of Consumption to GDP in the US.** Data from FRED."
#| code-fold: true
#| fig-width: 80%
plot(data.date, data.consumption ./ data.gdp, label=false, ylabel="Ratio C/Y",
size=(500, 309))
```
**AR(1) 過程** $\rho_z, \sigma_z$
生産関数の関数形から次の関係式が導けます.
$$
\log z_t = \log y_t - \alpha \log k_t - (1-\alpha) \log n_t.
$$
上で仮定したように $\alpha$ の値を定めると, $z_t$ の時系列データが得られます. そこから, 分散と自己相関を計算することで, $\rho_z$, $\sigma_z$ の値を推定できます. ここでは, @cooley1995 の値 $\rho_z = 0.95$, $\sigma_z = 0.007$ を用います.
## Simulation
### `MacroModelling.jl` によるシミュレーション
RBCモデルのシミュレーションを行います. シミュレーション1から実装するためには, プログラミングや線形代数の基礎知識が必要ですが, RBCやDSGEなどの有名なマクロモデルはそのシミュレーションを自動化するパッケージが数多く存在します. ここでは, Julia の `MacroModelling.jl` パッケージを用います. なお, 歴史的には (現在でも) Matlab の `Dynare` パッケージが広く使われていますが, Matlabを利用するにはライセンス料がかかります.
$$
\begin{aligned}
\phi\frac{1}{1-n_t} &= (1-\phi)\frac{z_t (1-\alpha)k_t^{\alpha} n_t^{-\alpha}}{c_t} \\
\frac{1-\phi}{c_t} &= \beta \mathbb{E}\left[\frac{(1-\phi)(z_{t+1}\alpha k_{t+1}^{\alpha-1}n_{t+1}^{1-\alpha} + 1-\delta)}{c_{t+1}}\middle| z_t\right] \\
k_{t+1} &= (1-\delta)k_t + z_t k_t^{\alpha} n_t^{1-\alpha} - c_t \\
\log z_{t+1} &= \rho_z \log z_t + \sigma_z \varepsilon_{t}
\end{aligned}
$${#eq-rbc-model}
`MacroModelling.jl` では上記のモデルを以下のように, ほとんどそのまま記述できます. 一つ注意点としては, $t$ 時点ですでに決定されている変数 ($k_t, z_t$) は $t-1$ 時点の変数として記述する必要があるということです. また, 後にIRFをプロットするために, investment $i_t$ と output $y_t$ は明示的にモデルの中で定義する必要があります.
```{julia}
#| label: model-rbc
@model RBC begin
ϕ / (1 - n[0]) = (1 - ϕ) * ((1 - α) * y[0] / n[0]) / c[0]
(1 - ϕ) / c[0] = β * (1 - ϕ) * (α * y[1] / k[0] + 1 - δ) / c[1]
k[0] = (1 - δ) * k[-1] + i[0]
y[0] = z[0] * k[-1]^α * n[0]^(1 - α)
i[0] = y[0] - c[0]
log(z[0]) = ρ_z * log(z[-1]) + σ_z * ε[x]
end
@parameters RBC begin
β = 0.99
ϕ = 0.6325
α = 0.36
δ = 0.025
ρ_z = 0.95
σ_z = 0.007
end
```
ここで行われているのは以下の3つのステップです.
1. Variable の認識
1. Non-stochastic steady state の計算
1. 線形化 (一次近似)
モデル上のパラメータ数が6 (`y`, `c`, `k`, `n`, `z`, `i`) であること, 状態変数が2つ (`k`, `z`) であること, ジャンプ変数が2つであること (`c`, `n`) であること, ショックが1つであること (`ε`) が正しく認識されています. 線形化および一次近似はここでは立ち寄らず, @sec-nk で詳しく説明します.
**Non-stochastic Steady State**
Non-stochastic steady state はその名の通り, ショックが存在しない場合の定常状態を指します. 具体的には @eq-rbc-model の式を用いて, 以下の連立方程式を解きます.
$$
\begin{aligned}
\phi\frac{1}{1-n} &= (1-\phi)\frac{(1-\alpha)k^{\alpha} n^{-\alpha}}{c} \\
\frac{1-\phi}{c} &= \beta \left[\frac{(1-\phi)( \alpha k^{\alpha-1}n^{1-\alpha} + 1-\delta)}{c}\right] \\
k &= (1-\delta)k + z k^{\alpha} n^{1-\alpha} - c \\
\log z &= \rho_z \log z + \sigma_z \cdot 0
\end{aligned}
$${#eq-steady-state-rbc}
今回のような単純なモデルでは, 解析解を求めることが可能ですが, 一般的には解析解がないため, 数値的に解く必要があります. `MacroModelling.jl` では, `get_steady_state` 関数を用いて簡単に計算できます.
```{julia}
#| label: steady-state-rbc
get_steady_state(RBC)
```
ここでは, steady state の値の他に, 各パラメータに対する偏微分も計算されています. 例えば, 余暇のウェイトである $\phi$ の増加に対して, 消費 $c$ や労働 $n$ が減少することがわかります.
**Simulation**
このモデルは以下のように簡単にシミュレーションできます.
```{julia}
#| label: plot-simulation-rbc
plot_simulation(RBC, periods=150);
```
ここでいうシミュレーションとは
- 初期値を与える. ここでは steady state の値
- ショックを与える. ここでは TFPショック $\varepsilon_t \sim \mathcal{N}(0, 1)$ を毎期与える
各経済変数が相関を持ちながら変化していく様子が見て取れます. 次節ではより詳しく評価を行います.
## Evaluation
### Impulse Response Function (IRF)
Impulse Response Function (IRF) は, ショックに対する経済変数の応答を示すグラフです. RBCモデルでは, TFPショックに対する経済変数の応答を調べることが一般的です. 具体的には
1. $t = 0$ の時点で TFP ショック $\varepsilon_{t} = 1$ を与える
2. $t = 1$ 以降の時点で TFP ショックはゼロに戻す. $\varepsilon_{t} = 0$
3. ショック後の経済変数がどう steady state に収束していくかを調べる
`MacroModelling.jl` では, `plot_irf` 関数を用いてIRFをプロットできます.
```{julia}
#| label: plot-irf-rbc
plot_irf(RBC, periods=150);
```
モデルを理解する上で, それぞれの経済変数の変化を言語化することが大切です.
- $z_t$: TFPショックにより, 生産性が一時的に上昇した後, $\rho_{z}$ に従って減少していく
- $y_t$: TFPショックにより生産性が上昇し, 生産量も一時的に増加する. その後, TFPの減少に伴い生産量も減少していく
- $c_t$: 生産の上昇に伴い (恒常所得仮説に従って緩やかに) 消費が増加する. その後, 生産の減少に伴い消費も減少していく
- $n_t$: TFPショックにより, 労働の限界生産性が上昇し, 即座に労働供給が増加する. その後, 豊かになった家計は余暇を増やすために労働供給を減少させる
- $i_t$: TFPショックにより, 資本の限界生産性が上昇し, 即座に投資が増加する. その後, 生産性の減少に伴い投資も減少していく
- $k_t$: 資本はストック変数であるため, フローである投資 $i_t$ の変化に応じて徐々に変化する
**$\rho_z$ の役割**
```{julia}
#| label: fig-irf-rhos
#| fig-cap: "IRFs with Different TFP Persistence $\\rho_z$."
#| code-fold: true
T = 150
irfs = [
get_irf(RBC, periods=T, parameters=(:ρ_z => ρ_z)) ./
collect(get_steady_state(RBC, parameters=(:ρ_z => ρ_z)))[:, 1]
for ρ_z in (0.95, 0.9, 0.5)
]
ps = Array{Plots.Plot,1}(undef, 4)
for (i, (idx, title)) in enumerate((
(5, L"Output $(y_t)$"), (1, L"Consumption $(c_t)$"),
(6, L"TFP $(z_t)$"), (4, L"Labor $(n_t)$")
))
ps[i] = plot(1:T, 100 .* irfs[1][idx, :, 1], label=L"\rho_z=0.95",
ylabel="% deviation from SS",
title=title,
ylabelfontsize=8)
plot!(ps[i], 1:T, 100 .* irfs[2][idx, :, 1], label=L"\rho_z=0.9", linestyle=:dash)
plot!(ps[i], 1:T, 100 .* irfs[3][idx, :, 1], label=L"\rho_z=0.5", linestyle=:dot)
end
plot(ps..., layout=(2, 2))
```
RBCモデルでは, TFPショックの自己回帰係数 $\rho_z$ が重要な役割を果たします. $\rho_z$ が大きいほど, ショックの影響が長く続くことを意味します. $y_t$ は $z_t$ に強く依存するため, $\rho_z$ が大きいほど $y_t$ の増加も長く続きます. また, 消費をスムーズにする働きから, $c_t$ の変化は $y_t$ より緩やかになります. 生産性の変化が長く続かないと予期している家計は, 初期の高い生産性を活かすために労働供給を増加させます. そのため, $\rho_z$ が小さいほど $n_t$ の初期反応が大きくなります.
### 景気循環統計
@sec-facts でみた, 景気循環の特徴を定量的に評価するために, シミュレーション結果から2次モーメントを計算します. 具体的には, 各経済変数の標準偏差, 自己相関係数, 相関係数を計算します. ポイントとしては
- シミュレーションのバーンイン期間 (burn-in period) を設ける. ここでは100期間
- シミュレーションの期間は実際のデータと同じ140期間
- 各経済変数の対数をとり, 周期成分をHPフィルターで抽出する. ここでは四半期データを想定して, $\lambda = 1600$ を使用
- 各経済変数の標準偏差, 自己相関係数, 相関係数を計算する
- シミュレーションを複数回行い, 結果を平均化する. ここでは250回のシミュレーションを行う
ここで大事なのは, シミュレーションの結果を実際のデータと同じように扱うと言うことです. そのため, 対数をとりHPフィルターを適用しています.
```{julia}
#| code-fold: true
#| label: tbl-stats-model
#| tbl-colwidths: [17.5, 17.5, 17.5, 17.5, 25]
#| tbl-cap: Business Cycle Statistics from RBC Model
#| output: asis
function sim_one(; burnin, periods, mdl=RBC, parameters=(:ρ_z => 0.95))
sim = get_simulation(mdl, periods=periods + burnin, levels=true,
parameters=parameters)
cs = sim[1, burnin+1:end]
is = sim[2, burnin+1:end]
ns = sim[4, burnin+1:end]
ys = sim[5, burnin+1:end]
zs = sim[6, burnin+1:end]
cycles = [hp_filter(log.(xs), 1600)[1] for xs in (ys, cs, is, ns, zs)]
std_mdl = [std(xs) for xs in cycles]
acor_mdl = [cor(xs[2:end], xs[1:end-1]) for xs in cycles]
cory_mdl = [cor(xs, cycles[1]) for xs in cycles]
df = DataFrame(
pars=["y", "c", "i", "n", "z"],
std=100 .* std_mdl,
std_rel=std_mdl ./ std_mdl[1],
acor=acor_mdl,
cory=cory_mdl
)
end
function get_table(; n_sim=250, burnin=100, periods=140)
df = sim_one(burnin=burnin, periods=periods)
for i in 2:n_sim
df_i = sim_one(burnin=burnin, periods=periods)
df = vcat(df, df_i)
end
result = combine(groupby(df, :pars),
[:std, :std_rel, :acor, :cory] .=> mean .=> [:std, :std_rel, :acor, :cory]
)
return result
end
df_mdl = get_table()
df_mdl.pars = ["Output", "Consumption", "Investment", "Labor", "TFP"]
pretty_table(
df_mdl,
column_labels=["Variable", "Std. Dev. (%)", "SD rel. to GDP",
"Autocorrelation", "Correlation with GDP"],
backend=:markdown,
allow_markdown_in_cells=true,
formatters=[(v, i, j) -> v isa Number ? @sprintf("%.3f", v) : v]
)
```
ここで @tbl-stats-data と @tbl-stats-model の結果を比較すると, RBCモデルは実際のデータの2次モーメントをよく再現していることが分かります. 特に,
- 消費と労働の標準偏差はGDPより小さい
- 投資の標準偏差はGDPより数倍大きい
ところは実際のデータをよく再現しています. ただし, GDP $y$ との相関は, 実際のデータよりも大きくなっています. これは, RBCモデルが TFPショックに対して非常に敏感であるためです.
RBCモデルはとてもシンプルなモデルですが, 実際のデータの景気循環をよく再現することが分かります. そのため, RBCモデルを土台として, モデルを拡張することで, より現実的なモデルを構築することができます. 代表的な研究としては, 以下のように発展していきます.
- 個人の異質性: @aiyagari1994
- 金融の役割: [New Keynesian](/02-nk.qmd) モデル
- 失業の役割: @merz1995; @andolfatto1996